標準偏差とは?高校数学に再トライ!
意外と実社会で使うことが多い標準偏差。
高校の時には意味も分からず公式だけ覚えてたので、今になって改めて定義を理解してみます!
標準偏差は平均値から順番に理解するべし
標準偏差を理解するには平均値から順番に確認すると分かりやすいです。以下に平均値、偏差、分散、標準偏差の計算方法を順に説明していきます。
平均とは?
平均とはいくつかの値があった場合の重心のような値です。とある4人がとあるテストをした点数が、「50点、60点、80点、90点」であった場合、平均値は下記。
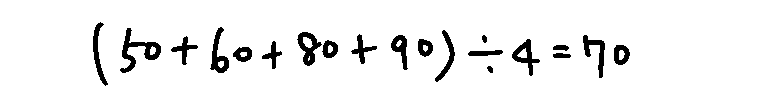
平均は70となりました。これは簡単です。
偏差とは?
偏差とは各標本と平均値の差です。同じく「50点、60点、80点、90点」の場合で偏差を計算すると下記。
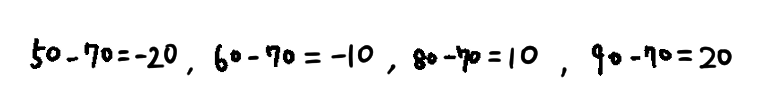
偏差は各標本が平均よりもどれだけ上か下かをシンプルに表した値です。標準偏差まではあと2段階計算を行います。
分散とは?
分散とはいくつかの値の集団のばらつきの程度を示す値です。各値の平均値からの差(=偏差)の二乗を平均したものです。平均の時と同じく「50点、60点、80点、90点」の例で計算した分散は下記。
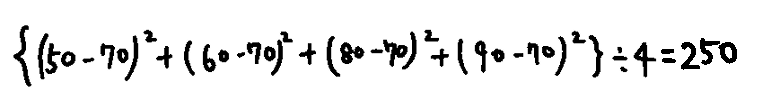
上記のようにこの場合の分散は250でした。でも50点や60点のテストの話をしているのに、分散は250でしたと言ってもいまいちピンときません。それは分散の値は二乗されているので、もとになっているテストの点数に比べて値が大きすぎるためです。それを解消して実感のある値にしたのが次の標準偏差です。
標準偏差とは?
標準偏差も分散と同じく、いくつかの値のばらつきの程度を示す値です。標準偏差は分散の平方根の値です。つまり分散は二乗されていてピンとこない値だったので、平方根で二乗をとっぱらって、実感できる値にしたものです。先ほどの分散の値250から標準偏差を求めると下記。
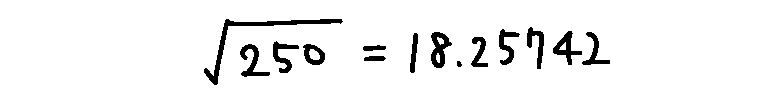
標準偏差は約18となりました。この値ならば「50点、60点、80点、90点」のばらつきの程度として実感しやすい値です。
参考:「平均偏差」はなぜ使われないのか?
標準偏差と似た値に、「平均偏差」というものがあります。平均偏差は、各標本値と平均値の差(=偏差)の絶対値を平均したもの。上と同じく「50点、60点、80点、90点」の例で計算すると下記の通り。
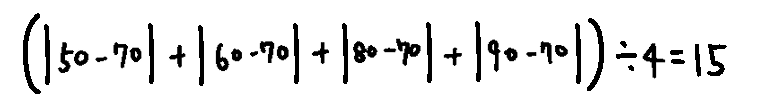
標準偏差が18.25…なのに対して、平均偏差は15と、ある程度似た値を示します。計算式からは、標準偏差よりも平均偏差の方がよりばらつきの程度をシンプルに表していると言えます。それでも平均偏差はあまり使われることはありません。その理由は標準偏差の方が統計学的に活用しやすいからだと言われています。具体的には、標準偏差を使うことで、どの程度のばらつきの中に何%の標本が含まれるかを推測できたり、最小二乗法によって回帰直線を得ることができるなどがあります。つまり平均偏差よりも標準偏差の方が圧倒的に実用上の利便性が高いため平均偏差の出番が無いのです。
